2008 Projects:
 | Matrix Factorization (number theory) |
| Project Director: Vadim Ponomarenko |
The "fundamental theorem of arithmetic" tells us that all integers ≥ 2 can be expressed as a product of primes, and that this product is unique (up to commutativity). Suppose we replace "integers" by "matrices"; is there an analogous theorem? The answer depends on the details -- for example we need an appropriate analog of "prime".
A forty-year-old paper considers the special case of 2x2 matrices, with entries nonnegative integers, and with determinant one. In this case, every such matrix has a factorization into two specific "prime" matrices L and R, and this factorization is unique. Note that this is stronger than the fundamental theorem of arithmetic -- since there is no commutativity, the factorization is completely unique, period. That same paper also considers the similar case where "nonnegative" is replaced by "positive". For any specific such matrix, if its smallest entry is 1, it is "prime"; if its smallest entry is 2, it factors uniquely as a product of primes; if its smallest entry is 3 or more, it possesses neither of these properties.
Very little progress has been made since that paper on this problem, probably because the context is noncommutative -- much work has been done on factorization of commutative rings. Our research will be on the problem of matrix factorization.. In certain circumstances, there may be unique factorization. In other circumstances, there may not be unique factorization, but we can still measure how badly this fails.
 | Theoretical Studies in Cell Migration (biomathematics) |
| Project Director: Diana Verzi |
|
Cell migration is an important behavior in wound healing, morphogenesis and cancerogenesis. It is based on a complex mechanochemical protein machine, regulated and self-organized by a complex network of biochemical reactions. The best way to elucidate principles of cell migration these complex cells is to choose a specific system and attempt a complete understanding of its working. Our work will focus on the migrating amoeboid sperm of the nematode Ascaris suum. These cells move using a simpler mechanical engine based upon a network of major sperm protein. More to the point, their motion is similar to similarly shaped actin-based cells.
Physical principles of protrusion, adhesion and contraction will be applied to a dynamic cytoskeletal system within the crawling cell, resulting in a system of partial differential equations. We will extend the work of an earlier study in one dimension to a two-dimensional model using polar coordinates. Students will contribute to theoretical and numerical formulation and perform simulations in MATLAB to consider motion, morphology, and directional response to external signaling. They will create a presentation and contribute to a publishable paper. Please indicate any coursework in physics, computer science, or biology in your application materials. | 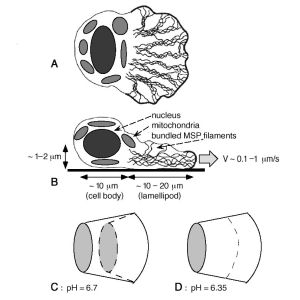 |









